

Brescia, gennaio 2006
Logica, probabilità e combinatoria:
Soluzione del problema 8
Sia
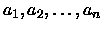 una successione arbitraria di interi
positivi. Si prenda a caso un elemento della successione e sia
una successione arbitraria di interi
positivi. Si prenda a caso un elemento della successione e sia 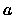 il suo valore.
Si prenda a caso un altro elemento, indipendentemente dal primo e sia
il suo valore.
Si prenda a caso un altro elemento, indipendentemente dal primo e sia 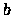 il suo valore.
Poi un terzo, di valore
il suo valore.
Poi un terzo, di valore 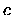 .
Dimostrare che la probabilità che
.
Dimostrare che la probabilità che 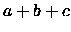 sia divisibile per
sia divisibile per 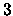 è almeno
è almeno 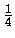 .
.
Dimostrazione
Data la sequenza
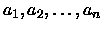 con
con
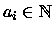 ,
scegliamo in modo casuale tre elementi di valore
,
scegliamo in modo casuale tre elementi di valore 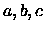 .
Vogliamo calcolare la probabilità che
.
Vogliamo calcolare la probabilità che
Siano:
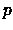 la probabilità di un intero positivo di essere congruo a
la probabilità di un intero positivo di essere congruo a 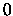 modulo
modulo 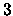 ;
;
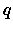 la probabilità di un intero positivo di essere congruo a
la probabilità di un intero positivo di essere congruo a 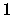 modulo
modulo 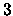 ;
;
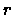 la probabilità di un intero positivo di essere congruo a
la probabilità di un intero positivo di essere congruo a 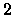 modulo
modulo 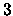 .
.
Perché sia
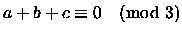 , deve verificarsi uno dei due casi:
, deve verificarsi uno dei due casi:
-
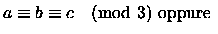
-
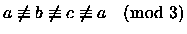
- La probabilità che
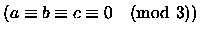 è
è 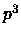 ,
,
la probabilità che
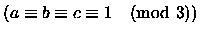 è
è 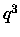 ,
,
la probabilità che
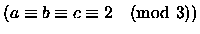 è
è 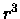 .
.
Quindi la probabilità che
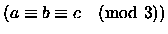 è
è 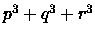 .
.
- I casi favorevoli sono
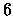 :
:
- -
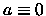 ,
, 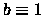 ,
, 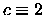 ;
;
- -
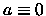 ,
, 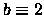 ,
, 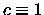 ;
;
- -
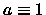 ,
, 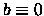 ,
, 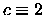 ;
;
- -
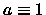 ,
, 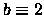 ,
, 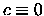 ;
;
- -
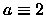 ,
, 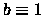 ,
, 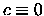 ;
;
- -
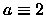 ,
, 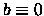 ,
, 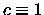 ;
;
Ognuno di essi ha probabilità
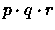 . In totale allora:
. In totale allora:
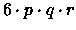
Resta da vedere che
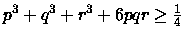 .
.
Poiché 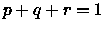 , si ha:
, si ha:
Quindi bisogna dimostrare la seguente disuguaglianza:
che equivale a:
Equivalentemente, ricordando che 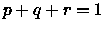 :
:
Se
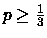 , allora
, allora
è massimo per 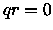 e
e 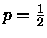 .
In questo modo si ha
.
In questo modo si ha
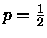 ,
, 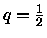 e
e 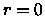 , oppure
, oppure
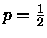 ,
, 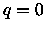 e
e
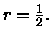
Per simmetria, non si perde di generalità se si suppone
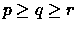 , per cui dev'essere
, per cui dev'essere
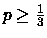 .
Allora il valore minimo di
.
Allora il valore minimo di
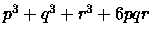 è
è 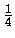 .
.
This document was generated using the
LaTeX2HTML translator Version 2002 (1.62)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -no_antialias_text Pb8.tex
The translation was initiated by DMF Web on 2006-01-10


DMF Web
2006-01-10
![]() una successione arbitraria di interi
positivi. Si prenda a caso un elemento della successione e sia
una successione arbitraria di interi
positivi. Si prenda a caso un elemento della successione e sia ![]() il suo valore.
Si prenda a caso un altro elemento, indipendentemente dal primo e sia
il suo valore.
Si prenda a caso un altro elemento, indipendentemente dal primo e sia ![]() il suo valore.
Poi un terzo, di valore
il suo valore.
Poi un terzo, di valore ![]() .
Dimostrare che la probabilità che
.
Dimostrare che la probabilità che ![]() sia divisibile per
sia divisibile per ![]() è almeno
è almeno ![]() .
.