Disfida Matematica 2007
Soluzione del problema 19
- 19.
- Ritorno al passato. Proviamo a contare le
permutazioni delle cifre da 1 a 9 in modo che al terzo, al sesto e
al nono posto ci sia una cifra pari. In questo modo avremo le terne
di numeri pari di tre cifre. Indicando con
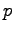 una cifra pari e con
una cifra pari e con
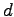 una cifra dispari, e osservando che il numero di
una cifra dispari, e osservando che il numero di 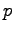 è 4 e il
numero di
è 4 e il
numero di 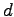 è 5, si ha
è 5, si ha
Togliamo per un attimo le tre 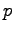 : restano 6 buchi in cui disporre 5
: restano 6 buchi in cui disporre 5
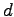 (scelte tra 5) e una
(scelte tra 5) e una 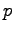 (scelta tra 4); per fare questo ci sono
esattamente
(scelta tra 4); per fare questo ci sono
esattamente
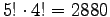 modi distinti. Combinando questi con i
modi distinti. Combinando questi con i 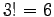 modi di disporre le tre
modi di disporre le tre 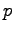 finali, si hanno in tutto
finali, si hanno in tutto
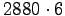 modi. Poiché però il testo dice che i tre numeri di tre cifre
vanno presi ordinati (perché la Noblità avrà sempre quello più
alto, il Clero quello in mezzo e il Terzo Stato quello più basso),
tutti questi modi vanno quozientati con il numero di possibili
riordinamenti di 3, che è di nuovo
modi. Poiché però il testo dice che i tre numeri di tre cifre
vanno presi ordinati (perché la Noblità avrà sempre quello più
alto, il Clero quello in mezzo e il Terzo Stato quello più basso),
tutti questi modi vanno quozientati con il numero di possibili
riordinamenti di 3, che è di nuovo 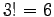 , e dunque il numero totale
è
, e dunque il numero totale
è
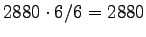 . La risposta è quindi
. La risposta è quindi
 .
.
DMF Web
2007-03-29