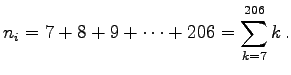
(Nota: tale numero si può calcolare facilmente, e fa
Inoltre, dopo il ribaltone nessun gruppo parlamentare può avere più di 200 parlamentari, altrimenti ce ne sarebbero due che prima appartenevano allo stesso gruppo. Quindi il numero di parlamentari che appartengono ad uno dei nuovi gruppi (ovvero che NON sono diventati indipendenti) è al massimo
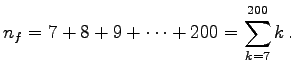
(Anche qui è facile, ma inutile, calcolarlo:
Quindi il numero di parlamentari che sono diventati indipendenti deve essere almeno
Ora bisogna dimostrare che c'è almeno un modo di ridistribuire i parlamentari come richiesto.
Supponendo che i parlamentari siano proprio in numero di ![]() , e
quindi che i vecchi gruppi parlamentari coprissero tutti i numeri da 7
a 206, si può fare così: si numerano da 1 in avanti tutti i
componenti di ciascun gruppo prima del ribaltone, si scartano tutti i
numeri da 1 a 6 e si mettono insieme tra loro tutti i numeri 7, tutti
i numeri 8 e così via, fino fino a mettere insieme tutti i numeri
200 (che sono proprio 7). Infine, si scartano tutti i numeri dal 201
in poi. In questo modo si sono scartati esattamente
, e
quindi che i vecchi gruppi parlamentari coprissero tutti i numeri da 7
a 206, si può fare così: si numerano da 1 in avanti tutti i
componenti di ciascun gruppo prima del ribaltone, si scartano tutti i
numeri da 1 a 6 e si mettono insieme tra loro tutti i numeri 7, tutti
i numeri 8 e così via, fino fino a mettere insieme tutti i numeri
200 (che sono proprio 7). Infine, si scartano tutti i numeri dal 201
in poi. In questo modo si sono scartati esattamente
![]() parlamentari, che saranno gli
indipendenti, e tutti i nuovi gruppi hanno un numero diverso di
persone e maggiore o uguale di 7. Quindi la risposta è
parlamentari, che saranno gli
indipendenti, e tutti i nuovi gruppi hanno un numero diverso di
persone e maggiore o uguale di 7. Quindi la risposta è
![]() .
.