L'equazione.
Se
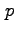 è un primo che divide
è un primo che divide
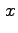 (
(
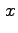 è una soluzione intera della equazione), si ha che
è una soluzione intera della equazione), si ha che
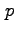 divide i primi due termini dell'equazione, e quindi
deve dividere
divide i primi due termini dell'equazione, e quindi
deve dividere
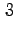 (il terzo termine). Gli unici valori
possibili per
(il terzo termine). Gli unici valori
possibili per
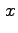 sono dunque
sono dunque
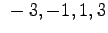 ,
dopo aver escluso anche le potenze di
,
dopo aver escluso anche le potenze di
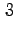 per la stessa
ragione.
per la stessa
ragione.
A questo punto si potrebbe gia procedere per tentativi provando
a sostituire a
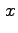 ciascuno di questi quattro valori;
in alternativa si può restringere ulteriormente il campo
procedendo come segue.
Riducendo l'equazione modulo
ciascuno di questi quattro valori;
in alternativa si può restringere ulteriormente il campo
procedendo come segue.
Riducendo l'equazione modulo
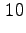 si ottiene
si ottiene
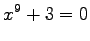 mod mod 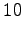 |
(1) |
dove il termine di grado
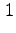 in
in
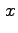 non è presente perché il testo
specifica che il coefficiente sconosciuto è multiplo di
non è presente perché il testo
specifica che il coefficiente sconosciuto è multiplo di
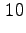 e
quindi congruo a
e
quindi congruo a
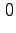 modulo
modulo
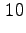 .
Ora è necessario sfruttare una versione del piccolo teorema di
Fermat che asserisce che
.
Ora è necessario sfruttare una versione del piccolo teorema di
Fermat che asserisce che
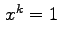 mod
mod 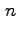 se
se
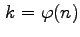 e
e
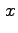 è primo con
è primo con
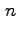 ;
;
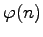 è la funzione di Eulero, che conta il numero di
interi positivi minori di
è la funzione di Eulero, che conta il numero di
interi positivi minori di
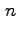 che sono primi con
che sono primi con
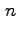 .
Per numeri
.
Per numeri
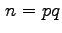 con
con
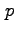 e
e
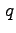 primi la funzione
primi la funzione
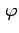 può
essere esplicitata come
può
essere esplicitata come
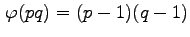 e quindi
e quindi
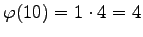 .
Nel caso specifico
.
Nel caso specifico
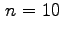 si può anche elencare agevolmente
tutti i numeri minori di
si può anche elencare agevolmente
tutti i numeri minori di
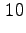 e primi con
e primi con
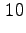 :
:
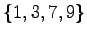 , che sono proprio i valori di
, che sono proprio i valori di
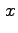 (considerati
modulo
(considerati
modulo
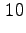 ) che sono stati isolati in precedenza.
) che sono stati isolati in precedenza.
Il piccolo teorema di Fermat quindi implica che (lavorando
sempre modulo
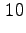 ):
):
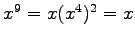 , da cui si ricava
, da cui si ricava
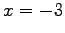 mod
mod 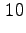 o equivalentemente
o equivalentemente
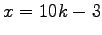 per un qualche
per un qualche
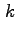 intero (positivo, negativo o nullo).
intero (positivo, negativo o nullo).
L'unico valore di
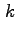 compatibile con le possibili scelte di
compatibile con le possibili scelte di
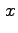 viste all'inizio è
viste all'inizio è
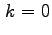 , ovvero
, ovvero
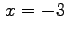 .
Indicando con
.
Indicando con
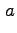 il coefficiente incognito,
la sostituzione
il coefficiente incognito,
la sostituzione
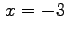 porta a
porta a
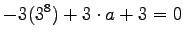 |
(2) |
e semplificando per
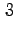 otteniamo
otteniamo
La risposta è dunque
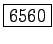 .
.
![]() ciascuno di questi quattro valori;
in alternativa si può restringere ulteriormente il campo
procedendo come segue.
Riducendo l'equazione modulo
ciascuno di questi quattro valori;
in alternativa si può restringere ulteriormente il campo
procedendo come segue.
Riducendo l'equazione modulo
![]() si ottiene
si ottiene
![]() ):
):
![]() , da cui si ricava
, da cui si ricava
![]() mod
mod ![]() o equivalentemente
o equivalentemente
![]() per un qualche
per un qualche
![]() intero (positivo, negativo o nullo).
intero (positivo, negativo o nullo).
![]() compatibile con le possibili scelte di
compatibile con le possibili scelte di
![]() viste all'inizio è
viste all'inizio è
![]() , ovvero
, ovvero
![]() .
Indicando con
.
Indicando con
![]() il coefficiente incognito,
la sostituzione
il coefficiente incognito,
la sostituzione
![]() porta a
porta a